문제 설명

문제 링크: https://www.acmicpc.net/problem/2166
풀이
이 문제는 다각형의 면적을 소수점 첫째 자리까지 출력하는 문제입니다.
다각형의 면적을 구하는 가장 간단한 방법은 다각형을 삼각형으로 분해해서, 삼각형을 면적을 합하는 방법입니다.
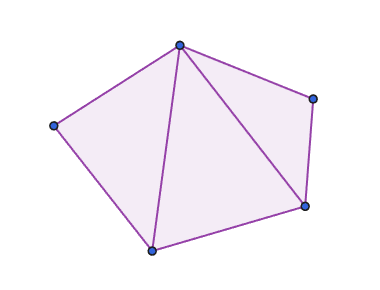
그러나, 이러한 방식은 볼록 다각형의 경우에만 사용할 수 있는 방법입니다.

위의 이미지 같은 오목 다각형의 경우, 면적을 구하려면 전체 다각형을 삼각형으로 나눠서 더한 면적에서, 흰 부분의 삼각형 면적을 빼야 합니다.
그런데, 어떤 기준으로 푸른 부분의 삼각형은 더하고, 흰 부분의 삼각형을 뺄 수 있을까요?
그 기준은, 삼각형을 이루는 변을 벡터로 변경했을 때 생성되는 벡터들이 회전하는 방향입니다.

푸른색 부분의 삼각형들을 이루는 벡터는 시계 반대 방향으로 회전하는 반면, 흰색 부분의 삼각형은 시계 방향으로 회전하는 것을 볼 수가 있습니다.
따라서, 시계 반대 방향으로 회전하는 방향을 가진 삼각형의 면적은 합치고, 그 반대 방향일 땐 면적을 빼면 오목 다각형의 면적까지 구할 수 있을 것입니다.
이러한 방향을 수학적으로 표현할 수 있는 도구가 바로 벡터의 외적( Cross Product )입니다.
벡터의 외적은 주어진 두 벡터 A(a1, a2, a3)와 B(b1, b2, b3)에 직각인 벡터를 말합니다.
이 외적 벡터는 A와 B 벡터가 회전하는 방향에 따라 방향이 달라지기 때문에,
벡터의 외적을 구하면 A와 B 벡터가 회전하는 방향을 알 수 있습니다.

이 외적의 방향을 벡터 A, B가 구성하는 평면 P의 방향이라고 합니다.
그리고, 벡터 A, B가 만드는 삼각형은 평면 P에 속하므로, 이 삼각형의 방향이기도 합니다.
또한, 이 외적의 크기는 A, B가 만드는 사각형의 넓이입니다.
벡터 A (a1, a2, a3)와 B (b1, b2, b3)에 대하여,
벡터의 외적은
$\overrightarrow{A}~x~ \overrightarrow{B}~=~ ( a_2 x b_3 - a_3 x b_2, a_3 x b_1 - a_1 x b_3, a_1 x b_2 - a_2 x b_1 )$
입니다.
이러한 벡터의 외적을 2차원 평면 좌표에 도입하면,
삼각형을 이루는 벡터 A (a1, a2, 0)와 B (b1, b2, 0)의 외적은
$\overrightarrow{A}~x~ \overrightarrow{B}~=~ ( 0, 0, a_1 x b_2 - a_2 x b_1 )$
이 되고, 이 벡터의 방향은 z 축 성분 $a_1 x b_2-a_2 x b_1$의 부호를 통해서 알 수 있습니다.
만약, 위 벡터의 z좌표가 양수라면, A와 B 벡터가 반시계 방향으로 회전한다는 것을 말합니다.
그리고 외적의 크기인 $\left| a_1 x b_2-a_2 x b_1 \right|$는 이 두 벡터가 만드는 사각형의 면적이 됩니다.
( 2차원에선 z 성분만 값이 있고, x,y 성분의 값은 0입니다.)
이제, 이러한 정보를 가지고,
입력된 다각형을 삼각형으로 나눠서, 세 정점으로부터 벡터를 구하고,
이 벡터들을 이용해 벡터의 외적을 구하면 됩니다.
typedef double MREAL;
// 삼각형의 세 정점으로부터 벡터의 외적을 구하는 함수
// 벡터의 외적의 크기는 벡터들이 만드는 사각형의 넓이
inline MREAL CrossProduct( MREAL x0, MREAL y0, MREAL x1, MREAL y1, MREAL x2, MREAL y2){
MREAL v1 = x1 - x0, v2 = x2 - x1;
MREAL u1 = y1 - y0, u2 = y2 - y1;
// 2차원에서 z성분만 값이 있고, x,y성분은 0입니다.
return v1*u2 - v2*u1;
}
int main(){
MREAL rArea = 0;
int N = readInt();
int x[3], y[3];
x[0] = readInt();
y[0] = readInt();
x[1] = readInt();
y[1] = readInt();
for(int i = 2; i < N; i++){
x[2] = readInt();
y[2] = readInt();
rArea += CrossProduct( x[0], y[0], x[1], y[1], x[2], y[2]);
x[1] = x[2];
y[1] = y[2];
}
rArea = fabs(rArea / 2.0f); // 삼각형의 면적을 구해야 하므로 나눔
rArea *= 10.0f;
rArea = round(rArea); // 소수점 두째 자리에서 반올림
rArea /= 10.0f;
printf("%.1lf", rArea);
return 0;
}벡터의 외적 값이 음수로 나오면, 삼각형의 방향이 반대를 가리키는 것이므로,
그대로 음수를 더하는 계산을 해야 합니다.
마지막으로, round 함수가 소수점 첫째 자리에서 반올림하기 때문에,
소수점 둘째 자리에서 반올림하기 위해서 10을 곱했다 다시 나누었습니다.
소스 코드
#include <iostream>
#include <cmath>
#include <vector>
using namespace std;
// 입출력 소스 --------------------------------------------
#define WBUF_SIZE (1 << 20)
char rbuf[WBUF_SIZE];
int ridx, nidx;
inline char read() {
if (ridx == nidx) {
nidx = fread(rbuf, 1, 1 << 20, stdin);
if (!nidx) return 0;
ridx = 0;
}
return rbuf[ridx++];
}
inline int readInt() {
int sum = 0;
char now = read();
bool flg = false;
while (now <= 32) now = read();
if (now == '-') flg = true, now = read();
while (now >= 48) sum = sum * 10 + now - '0', now = read();
return flg ? -sum : sum;
}
//----------------------------------------------------------
typedef double MREAL;
inline MREAL CrossProduct( MREAL x0, MREAL y0, MREAL x1, MREAL y1, MREAL x2, MREAL y2){
MREAL v1 = x1 - x0, v2 = x2 - x1;
MREAL u1 = y1 - y0, u2 = y2 - y1;
return v1*u2 - v2*u1;
}
int main(){
MREAL rArea = 0;
int N = readInt();
int x[3], y[3];
x[0] = readInt();
y[0] = readInt();
x[1] = readInt();
y[1] = readInt();
for(int i = 2; i < N; i++){
x[2] = readInt();
y[2] = readInt();
rArea += CrossProduct( x[0], y[0], x[1], y[1], x[2], y[2]);
x[1] = x[2];
y[1] = y[2];
}
rArea = fabs(rArea / 2.0f);
rArea *= 10.0f;
rArea = round(rArea);
rArea /= 10.0f;
printf("%.1lf", rArea);
return 0;
}
'문제 풀이 > 백준 (BOJ)' 카테고리의 다른 글
| [백준/BOJ] 1766번: 문제집 ( 위상 정렬 ) - C++ 문제 풀이 (0) | 2024.07.14 |
|---|---|
| [백준/BOJ] 2252번: 줄 세우기( 위상 정렬, Topology Sort ) - C++ 문제 풀이 (0) | 2024.07.14 |
| [백준/BOJ] 4386번: 별자리 만들기 ( Prim 알고리즘 ) - C++ 문제 풀이 (0) | 2024.07.05 |
| [백준/BOJ] 1197번: 최소 스패닝 트리( Minimal Spanning Tree ) - C++ 문제 풀이 (0) | 2024.07.04 |
| [백준/BOJ] 4195번: 친구 네트워크 ( Union-Find 알고리즘 ) - C++ 문제 풀이 (0) | 2024.07.04 |





