문제 설명


문제 링크: https://www.acmicpc.net/problem/12865
풀이
N개의 물품 중에서 K 무게를 넘지 않도록 물품들을 배낭에 담았을 때, 담긴 물품들의 최대 가치값의 합은 얼마인가를 물어보는 문제이다.
배낭 문제라고 동적 계획법을 사용하는 유명한 문제이다.
동적 계획법이란 전체의 문제를 작은 부분 문제로 나누어 계산한 후, 이 계산한 결과를 사용하여 전체의 문제를 빠르게 푸는 방법이다.
이 방법은 부분 문제를 어떻게 규정해야 하는가가 가장 어려운 부분이라고 할 수 있다.
여기서는 부분 문제를 "N-1개의 물품 중에서 K 무게를 넘지 않도록 담았을 때, 최대 가치값의 합은 얼마인가?"로 잡았다.
일단, 물품의 수를 계속 줄여가다 1개까지 줄어들면 계산은 아주 간단해진다.
그리고 N-1 물품을 사용해서 이미 계산을 했기 때문에, N개의 물품을 사용할 때의 계산은 마지막 물품을 어떻게 사용해야 하는가만 생각하면 된다.
간단한 문제로부터 일반 계산식을 찾아보자.
물품의 개수 N=2, 무게 K = 8
첫 번째 물품의 무게 w1 = 3, 가치 v1 = 14
두 번째 물품의 무게 w2 = 5, 가치 v2 = 11 일 때,
최대 가치의 합은 얼마인가라는 문제를 풀어보자.
우선, 용어 정리부터 필요할 것 같다.
wi는 i번째 물품의 무게 ( i = 1... N )
vi는 i번째 물품의 가치 ( i = 1... N )
N개의 물품에서 K 무게를 넘지 않았을 때, 최대 가치값의 합을 V(N, K)라고 하자.
그럼 첫 번째 물품의 무게 (w1=3)가 8을 넘지 않을 때, 최대 가치값이 14 임을 다음과 같이 쓸 수 있다.
V(1,8) = 14
참고로,
V(1,1) = 0
V(1,2) = 0
V(1,3) = 14
V(1,4) = 14... V(1,7) = 14이다.
그리고 두 번째 물품을 배낭에 넣었을 때 가치는 V(2,8) = V(1,8) + v2가 된다.
그렇지만, 위의 식은 조금 부족하다. 왜냐하면 v2를 합하기 위해, 두 번째 물품의 무게 w2가 쓰였다는 것을 알 수가 없기 때문이다.
이를 보완하면 V(2,8) = V(1,8-w2) + v2 = V(1,3) + v2이 된다.
이번엔 무게 K가 7일 때를 생각해 보자. ( w1 < K < w1+w2 )
V(2,7)은 v1과 v2에서 더 큰 가치를 선택해야 한다. 무게 때문에 두 물품을 모두 고를 수 없기 때문이다.
이를 식으로 하면 V(2,7) = max( V(1,7), v2 )라고 쓸 수 있다.
이제 두 경우를 포괄하면,
V(2,8) = max { V(1,8), V(1,3)+v2 }
V(2,7) = max { V(1,7), V(1,2)+v2 }가 된다.
그런데, 무게 K가 4일 때는 위의 식이 성립하지 않는다.
V(2,4) = max { V(1,4), V(1, -1)+v2 }가 되기 때문이다.
이런 의미 없는 식이 생기는 이유는 K가 w2 = 5보다 작기 때문이고, 이것은 w2 무게의 물품은 아예 배낭에 들어갈 수 없다는 얘기다.
이때의 공식은 V(2,4) = V(1,4) ( K < w2 일 때 )가 된다.
위의 모든 경우를 합한 일반식은 다음과 같다.
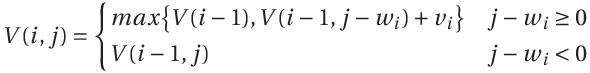
이제, i = 1, j = 1부터 시작해서 i = N, j = K까지 위의 식을 계산하여, 계산 값인 V(i, j)의 값을 차례로 cache [N+1][K+1] 버퍼에 채워가면서 최대 값을 구하면 문제 해결이다.
위의 식을 코드로 전환하면 다음과 같다.
#define ITEM_NUM 100 // N
#define MAX_WEIGHT 100000 // K
int cache[ITEM_NUM+1][MAX_WEIGHT+1];
int v[ITEM_NUM]; // value
int w[ITEM_NUM]; // weight
int maxValue = 0; // 최대값
for(int i = 1; i <= N; i++){ // 모든 물품을 계산하여, 최대값을 찾는다.
for( int j = 1; j <= K; j++){ // 모든 무게에 대하여
// 이전 계산 값을 이용하여, 현재 값을 계산
if ( w[i-1] <= j){
// 계산 된 값도, 다음 물품을 검사할 때 다시 사용된다.
cache[i][j] = max( cache[i-1][j], cache[i-1][j-w[i-1]] + v[i-1] );
}
else{
cache[i][j] = cache[i-1][j];
}
if ( cache[i][j] > maxValue)
maxValue = cache[i][j]; // 최대값을 구한다
}
}
}

소스 코드
#include <iostream>
using namespace std;
#define ITEM_NUM 100
#define MAX_WEIGHT 100000
int cache[ITEM_NUM+1][MAX_WEIGHT+1];
int v[ITEM_NUM];
int w[ITEM_NUM];
int main(){
ios::sync_with_stdio(false);
cin.tie(NULL);
int N, K, W, V;
cin >> N >> K;
int maxValue = 0;
for(int i = 0; i < N; i++){
cin >> W >> V;
w[i] = W; // weight
v[i] = V; // value
}
for(int i = 1; i <= N; i++){
for( int j = 1; j <= K; j++){
if ( w[i-1] <= j){
cache[i][j] = max( cache[i-1][j], cache[i-1][j-w[i-1]] + v[i-1] );
}
else{
cache[i][j] = cache[i-1][j];
}
if ( cache[i][j] > maxValue)
maxValue = cache[i][j];
}
}
cout << maxValue;
return 0;
}
'문제 풀이 > 백준 (BOJ)' 카테고리의 다른 글
| [백준/BOJ] 1463번: 1로 만들기 (동적 계획법) - C++ 문제 풀이 (0) | 2024.05.09 |
|---|---|
| [백준/BOJ] 1904번: 01 타일 (동적 계획법) - C++ 문제 풀이 (1) | 2024.05.06 |
| [백준/BOJ] 9184번: 신나는 함수 실행 ( 동적 계획법 ) - C++ 문제 풀이 (0) | 2024.04.30 |
| [백준/BOJ] 12789번: 도키도키 간식드리미 - C++ 문제 풀이 (0) | 2024.04.26 |
| [백준/BOJ] 24511번: queuestack - C++ 문제 풀이 (0) | 2024.04.24 |





